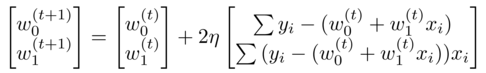Gradient descent

Minimize the Residual Sum of Squares

The slope & intercept can also be found via minimizing the RSS, which is a function of the slope (w₁) and intercept (w₀):

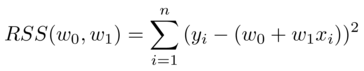
Finding the minimum or maximum corresponds to setting the derived function equal to zero.

KLAD For a concave or convex function there is only one point where there is a maximum or minimum, ie where the derivative equals zero. If a function is not concave nor convex, then it may have multiple maxima or minima.

Side-step: hill descent

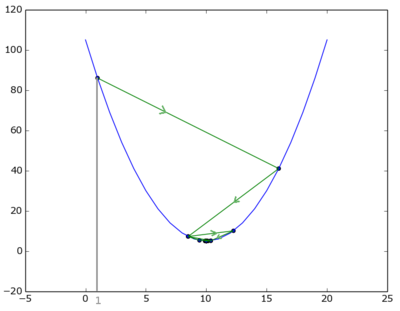
The gradient descent algorithm tries to find a minimum, in a step-wise fashion. This can easily be compared to the following hill descent for a simple parabole function, eg. y = 5 + (x-10)².

Hill descent with overshoot

Suppose you start at point x=1. To see if the function is going down or up we add a minute quantity, dx, and know that we are descending if f(x) > fx(x+dx).

Increment x with step=15.0, and look again at the direction in which the function is going. Here the direction has flipped, we have overshot our target, so for the next step we need to divide the step-size into half. Etc.

Keep doing this until the difference is smaller than a predefined constant.

To reach the result of 9.99999773021 required 57 iterations.

12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

step=15.0   # increment 
dx=1e-10    # miniscule value to check direction with, and to compare step with
x0=1.0      # start x 
x0d=is_down(x0,x0+dx)   # true if from x0 to x0+dx is going downhill
sgn=1.0     # add or subtract 

pt_v=[]     # store points in a list, for plotting
pt_v.append( (x0,fx(x0)) )  

count=0
while step>dx:
    x1=x0+sgn*step
    x1d=is_down(x1, x1+dx) 

    if x0d!=x1d:      # direction changed means overshoot
        step=step/2.0 # divide step by half

    sgn=1.0 if x1d else -1.0 

    x0=x1
    x0d=x1d
    pt_v.append( (x0,fx(x0)) )
    count+=1

print "Iterations: ", count,"  Result: ", x0

Hill descent without overshooting

The following algo is similar, but avoids overshooting: in case we overshoot, it keeps adjusting the step-size until we land on the left side of the minimum.

This time to get the result of 9.99999773022 required only 21 iterations, quite a bit better than above, but that of course may be due to the function and the choosen stepsize.

12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

step=15.0   # increment 
dx=1e-10    # miniscule value to check direction with, and to compare step with
x0=1.0      # start x
x0d=is_down(x0,x0+dx)   # true if from x0 to x0+dx is going downhill

pt_v=[]     # store points in a list, for plotting
pt_v.append( (x0,fx(x0)) )  

count=0
while step>dx:
    # keep dividing step by two until there is no overshoot
    while True:
        x1=x0+step
        x1d=is_down(x1, x1+dx) 
        if x0d==x1d:    # same direction
            break 
        step=step/2.0
    x0=x1
    x0d=x1d
    pt_v.append( (x0,fx(x0)) )
    count+=1

print "Iterations: ", count,"  Result: ", x0

The common functions for above code

Function and direction

5
6
7
8
9
10

# function (parabola)
def fx(x): 
    return 5 + (x - 10)**2

def is_down(x1, x2): 
    return True if fx(x1)>fx(x2) else False

Plotting

5
6
7
8
9
10

# function (parabola)
def fx(x): 
    return 5 + (x - 10)**2

def is_down(x1, x2): 
    return True if fx(x1)>fx(x2) else False

Mathematical approach

The above 2 solutions are the naive implementations, that perform fairly well. The mathematical way would be to calculate the next x as:

with step η typically chosen as 0.1.

During the ensuing iterations η can be kept constant or decreasing eg.

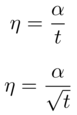
Choosing the stepsize is an art!

Gradient descent

Similarly to above, for gradient descent we update the coefficients by moving in the negative gradient direction (gradient is direction of increase). The increment in gradient descent is: