Run 1

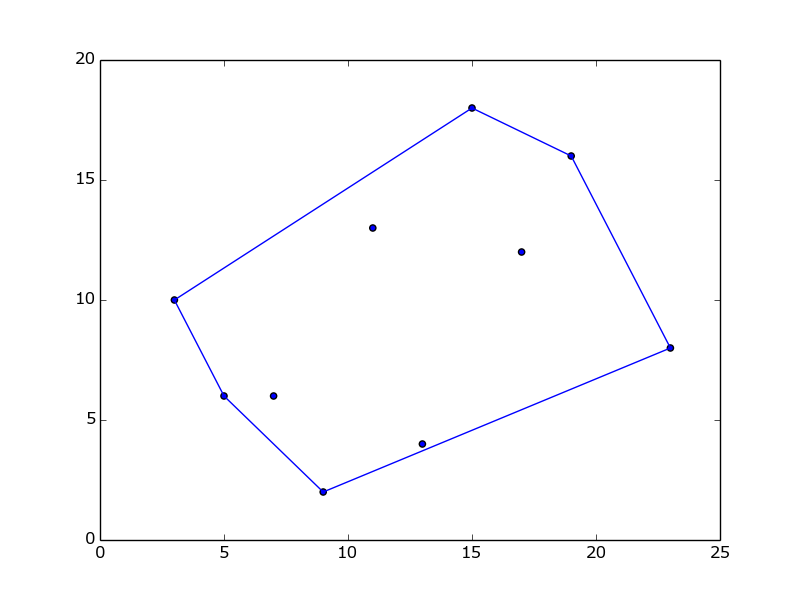
Input:

points= [ (9,2),(5,6),(3,10),(11,13),(7,6),(15,18),(19,16),(13,4),(23,8),(17,12)  ]

Output:

Points on the hull [(9, 2), (23, 8), (19, 16), (15, 18), (3, 10), (5, 6)]
Perimeter distance:  53.1991493831

Solution: the length of the wire we need to fence off the sheep is: 53.20.

Run 2

Check if the convex hull implementation is correct by taking as input a list of 1000 random points:

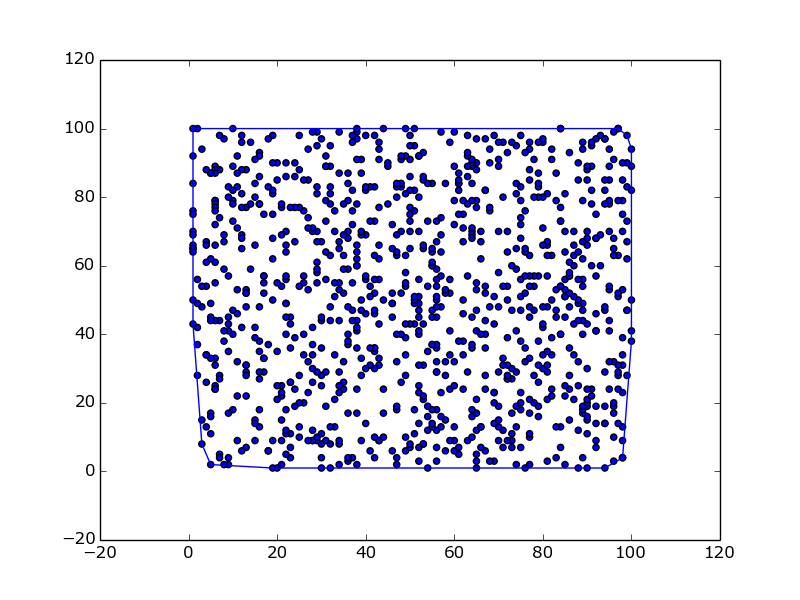
Conclusion: yes it's correct, all points fall within or on the convex hull.

Run 3

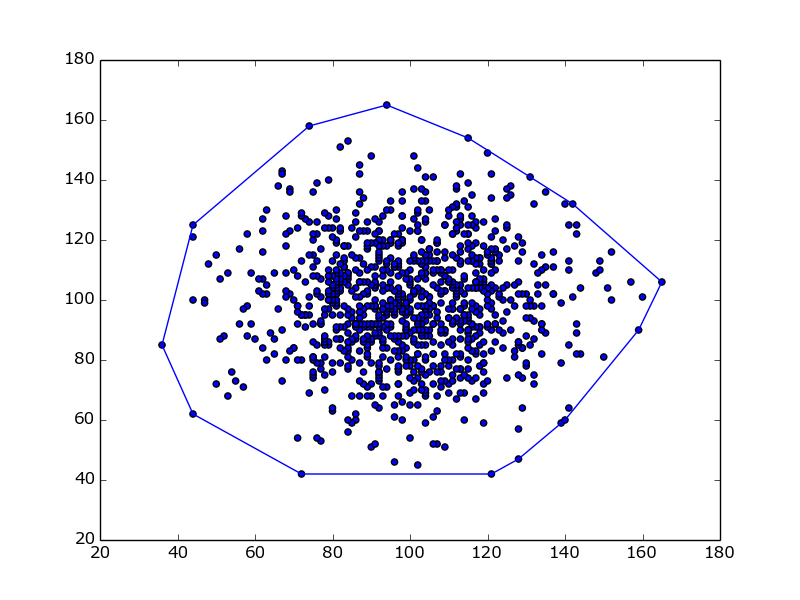
And finally, let's take as input a list of 1000 random points from a normal distribution:

Alternative implementation

Here is a different implementation of the core Graham scan, the same as implemented by Sedgewick in algs4.cs.princeton.edu/99hull/GrahamScan.java.html.

Because of the stack operations I find this implementation more difficult to understand, but its big advantage is that it doesn't need to copy the whole points list.

1
2
3
4
5
6
7
8
9

hulli=[]
hulli.append(0)
hulli.append(1)
for i in range(2,len(points)):
    top=hulli.pop()
    while clockwise( points[hulli[-1]], points[top], points[i])<=0:
        top=hulli.pop()
    hulli.append(top)
    hulli.append(i)